Correction commentée du partiel du lundi 2 avril 2001

1 1 point

Comment écririez-vous une expression équivalente à l'expression (or ( (foo x) 0) (integer? y)) dans un Scheme qui ne possèderait pas les formes spéciales and et or, mais seulement la forme if ? On conservera bien entendu la même complexité.

Solution :
(let ((test ( (foo x) 0))) (if test test (integer? y)))
Notes :
Cette solution est très générique, en ce sens qu'elle propose un motif que l'on pourrait répéter à volonté dans le cas d'une fonction n-aire. Elle tient notamment compte que or n'est pas vraiment un prédicat : il ne rend pas exclusivement #t ou #f, mais la première expression ne s'évaluant pas à #f, ou #f s'il n'y en a aucune.
Nous avons donc accepté les réponses similaires à la suivante (beaucoup plus simples dans le cas présent, il faut le reconnaître), vu que est réellement un prédicat renvoyant exclusivement #t ou #f :
(if ( (foo x) 0) #t (integer? y))) Profitons-en pour remarquer que, dans l'expression suivante, le second if est vraiment inutile et lourd :
(if ( (foo x) 0) #t (if (integer? y) #t #f))) En règle générale, soit de manière pratiquement indépendante du language, les expressions du style "if expr then true else false" sont très proche de la fonction "identité", et sont donc inutiles et alourdissent les programmes. En Scheme, une expression de la forme (if expr #t #f) ne sert qu'à projeter les valeurs différentes de #f vers #t, et #f vers #f...
Enfin, pour revenir à notre émulation de la forme spéciale or, notez bien que l'idée suivante :
(if ( (foo x) 0) ( (foo x) 0) (integer? y))) bien que proche de la réelle sémantique de or, évalue deux fois ( (foo x) 0), ce qui modifie non seulement la complexité, mais pourrait aussi conduire à un comportement complètement différent si foo (ou d'ailleurs) effectuaient des effets de bord (affichages, modifications de variables, ...) !

2 a 0.5 point

Donnez le résultat de l'évaluation au toplevel de l'expression suivante :
(let ((* (lambda (x y) (/ x y))) (/ (lambda (x y) (* x y)))) (* 6 (/ 3 2)))
Solution : let évalue les expressions des associations dans l'environnement englobant. Ce let lie donc localement le symbole * à la primitive /, et le symbole / à la primitive *. Le résultat de l'évaluation est donc 1.

b 0.5 point

Quel serait le résultat en remplaçant let par let* ?

Solution : let* est du sucre syntaxique pour une cascade de let réalisant chacun une seule association. Ce let* lie donc le symbole * à la primitive /, puis le symbole / à cette même primitive (via la liaison locale de *). Le résultat de l'évaluation est donc 4.

c 0.5 point

Quel serait le résultat en remplaçant let par letrec ?

Solution : letrec évalue les expressions des associations dans l'environnement du corps, prenant donc en compte les liaisons qu'il effectue. Ce letrec lie donc le symbole * à la fonction / locale, laquelle correspond à la fonction * locale. L'appel d'une des fonctions (en l'occurence, /) est remplacé par un appel à l'autre, qui est à son tour remplacé par un appel à l'une, etc., sans consommation de pile (ces deux fonctions locales étant récursives terminales) ; ce processus de remplacement ne peut donc pas s'arrêter de lui-même : l'évaluation boucle. Notons que, si les fonctions n'avaient pas été récursives terminales, l'évaluation de ce letrec aurait échoué tôt ou tard, par épuisement de la mémoire disponible.

3 On part de la fonction f définie par (define (f x y) (+ x y)). Par exemple (f 3 4) == 7.

a 1 point

Comment modifieriez-vous sa définition pour que l'on puisse l'invoquer sous la forme ((f x) y) ? Par exemple ((f 3) 4) == 7.

Solution :
(define (f x) (lambda (y) (+ x y)))

b 1 point

((f x y)) ? Par exemple ((f 3 4)) == 7.

Solution :
(define (f x y) (lambda () (+ x y)))

c 2 points

Au choix sous l'une des deux formes ((f x) y) ou (f x y) ? Par exemple ((f 3) 4) == (f 3 4) == 7.

Solution :
(define (f x . y) (if (null? y) (lambda (y) (+ x y)) (+ x (car y))))

4 a 0.5+0.5+0.5 points

Si l'on mesure le nombre d'appels à cons, quelle est la complexité de chacune des expressions suivantes, dans lesquelles L1, L2 et L3 sont trois listes ayant respectivements n₁, n₂, n₃ éléments ? L'une d'elles est-elle plus efficace ?
E == (append L1 (append L2 L3)) F == (append (append L1 L2) L3)
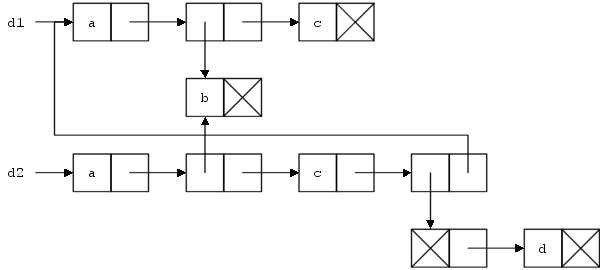
Solution : L'évaluation de E conduit à évaluer (append L2 L3), qui a une complexité en O(n₂) puis (append L1 L2+L3), qui a une complexité en O(n₁) ; la complexité complète est donc de O(n₁+n₂). L'évaluation de F conduit à évaluer (append L1 L2), qui a une complexité en O(n₁) puis (append L1+L2 L3), qui a une complexité en O(n₁+n₂) ; la complexité complète est donc de O(2n₁+n₂). Le calcul le plus efficace est donc celui de E.

b 1+2 points

Dessiner le diagramme des doublets et pointeurs en mémoire pour les chaînages de doublets d1 et d2 après qu'ils aient été définis par :
(define d1 '(a (b) c)) (define d2 (append d1 (cons (list '() 'd) d1)))
Solution :

5 On vous demander de programmer la fonction (delete x L) qui supprime toutes les occurences de l'élément x de la liste L. L'ordre des éléments non supprimés est conservé.
Exemple :
(delete 'si '(do si sol si si re fa)) -> (do sol re fa)

a 2 points

De manière récursive profonde :

Solution :
(define (delete x L) (cond ((null? L) '()) ((equal? (car L) x) (delete x (cdr L))) (else (cons (car L) (delete x (cdr L))))))

b 2 points

De manière itérative classique [sans CPS] :

Solution :
(define (delete x L) (define (iter L acc) (cond ((null? L) (reverse acc)) ((equal? (car L) x) (iter (cdr L) acc)) (else (iter (cdr L) (cons (car L) acc))))) (iter L '()))

c 2 points

A l'ordre supérieur, en une ligne :

Solution :
(define (delete x L) (filter (lambda (elt) (not (equal? x elt))) L))

d 2 points

En style CPS :

Solution :
(define (delete x L f) (cond ((null? L) (f '())) ((equal? (car L) x) (delete x (cdr L) f)) (else (delete x (cdr L) (lambda (Lkept) (f (cons (car L) Lkept)))))))

6 On définit un type abstrait "couple d'entiers naturels" avec le constructeur suivant :
(define ($cons x y) ; le "couple d'entiers naturels <x,y>" (* (expt 2 x) (expt 3 y))) On rappelle que (expt a b) retourne a^b.

a 2 points

Ecrire la fonction ($car c) prenant un tel "couple" c et retournant sa première composante :
> (define c ($cons 10 15)) > c 14693280768 > ($car c) 10
Solution :
(define ($car c) (if (zero? (modulo c 2)) (add1 ($car (quotient c 2))) 0))

b 1 point

Si l'on conserve le 2, aurait-on pu opter pour autre chose que 3 dans la définition de $cons ?

Solution :
$cons utilise la bijection¹ entre l'espace des paires d'entiers naturels et l'espace des entiers naturels de la forme 2^x.3^y, basée sur le thérorème selon lequel tout entier naturel peut s'écrire de manière unique sous la forme d'un produit de facteurs premiers et, inversement, tout entier naturel peut se décomposer de manière unique en produit de facteurs premiers². On peut donc remplacer 3 par tout nombre premier différent de 1 et 2, voire, dans le cas actuel, par tout entier premier avec 2. Il ne faut toutefois pas oublier que, si l'on peut considérer que le coût d'une division ou d'un modulo est constant lorsque l'on travaille sur des petits entiers (i.e. que le processeur sait traiter directement), cela n'est pas le cas pour les entiers longs, qui sont manipulés par la bibliothèque d'exécution de l'interprète/compilateur Scheme...

¹ Ce genre de bijection, ou, plus généralement, la représentation d'"objets" par des entiers s'apellant une Gödélisation.
² La seconde opération étant énormément plus coûteuse que la première, ce qui constitue les fondements de la cryptographie à base de clefs publiques/privées...


Dernière mise à jour : 02/04/2009 à 23:00